Что можно приготовить из кальмаров: быстро и вкусно

Вычислить сумму ряда можно только в случае, когда ряд сходится. Если ряд расходится то сумма ряда бесконечна и нет смысла что-то вычислять. Ниже приведены примеры из практики нахождения суммы ряда, которые задавали в Львовском национальном университете имени Ивана Франка. Задания на ряды подобраны так, что условие сходимости выполняется всегда, однако проверку на сходимость мы выполнять будем. Эта и следующие за ней статьи составляют решение контрольной работы по анализе рядов.

Пример 1.4 Вычислить сумму рядов:
а)
Вычисления: Поскольку граница общего члена ряда при номере следующему до бесконечности равна 0

то данный ряд сходится. Вычислим сумму ряда. Для этого преобразуем общий член, разложив его на простейшие дроби I и II типа. Методика разложения на простые дроби здесь приводиться не будет (хорошо расписана при интегрировании дробей), а лишь запишем конечный вид разложения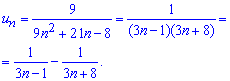

В соответствии с этим можем сумму расписать через сумму ряда образованного из простейших дробей, а дальше из разницы сумм рядов

Далее расписываем каждый ряд в явную сумму и выделяем слагаемые (подчеркивание), которые превратятся 0 после сложения. Таким образом сумма ряда упростится к сумме 3 слагаемых (обозначены черным), что в результате даст 33/40.

На этом базируется вся практическая часть нахождения суммы для простых рядов.
Примеры на сложные ряды сводятся к сумме бесконечно убывающих прогрессий и рядов, которые находят через соответствующие формулы, но здесь такие примеры рассматривать не будем.
б)
Вычисления: Находим границу n-го члена суммы

Она равна нулю, следовательно заданный ряд сходится и имеет смысл искать его сумму. Если граница отличная от нуля, то сумма ряда равна бесконечности со знаком "плюс" или "минус".
Найдем сумму ряда. Для этого общий член ряда который является дробью превратим методом неопределенных коэффициентов к сумме простых дробей I типа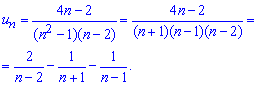

Далее по инструкции которая приводилась ранее записываем сумму ряда через соответствующие суммы простейших дробей

Расписываем суммы и выделяем слагаемые, которые станут равными 0 при суммировании.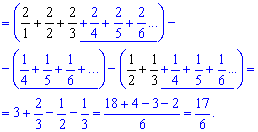

В результате получим сумму нескольких слагаемых (выделенные черным) которая равна 17/6 .

Пример 1.9 Найти сумму ряда:
а)
Вычисления: Вычислениям границы

убеждаемся что данный ряд сходится и можно находить сумму. Далее знаменатель функции от номера n раскладываем на простые множители, а весь дробь превращаем к сумме простых дробей I типа

Далее сумму ряда в соответствии с расписанием записываем через два простые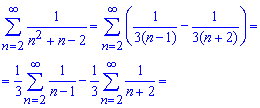

Ряды записываем в явном виде и выделяем слагаемые, которые после добавления дадут в сумме ноль. Остальные слагаемые (выделенные черным) и представляет собой конечную сумму ряда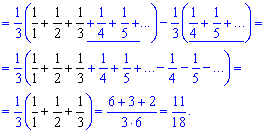

Таким образом, чтобы найти сумму ряда надо на практике свести под общий знаменатель 3 простых дроби.
б)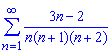
Вычисления: Граница члена ряда при больших значениях номера стремится к нулю

Из этого следует что ряд сходится, а его сумма конечна. Найдем сумму ряда, для этого сначала методом неопределенных коэффициентов разложим общий член ряда на три простейшего типа

Соответственно и сумму ряда можно превратить в сумму трех простых рядов

Далее ищем слагаемые во всех трех суммах, которые после суммирования превратятся в ноль. В рядах, содержащих три простых дроби один из них при суммировании становится равным нулю (выделен красным). Это служит своеобразной подсказкой в вычислениях

Сумма ряда равна сумме 3 слагаемых и равна единице.

Пример 1.15 Вычислить сумму ряда:
а)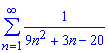

Вычисления: При общем член ряда стремящемся к нулю

данный ряд сходится. Преобразуем общий член таким образом, чтобы иметь сумму простейших дробей

Далее заданный ряд, согласно формулам расписания, записываем через сумму двух рядов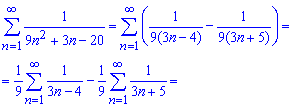

После записи в явном виде большинство членов ряда в результате суммирования станут равны нулю. Останется вычислить сумму трех слагаемых.

Сумма числового ряда равна -1/30 .
б)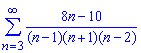
Вычисления: Поскольку граница общего члена ряда равна нулю,

то ряд сходится. Для нахождения суммы ряда разложим общий член на дроби простейшего типа.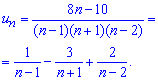

При разложении использовали метод неопределенных коэффициентов. Записываем сумму ряда из найденного расписание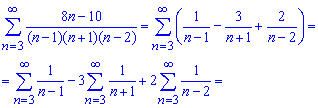

Следующим шагом выделяем слагаемые, не вносящие никакого вклада в конечную сумму и остальные оставшиеся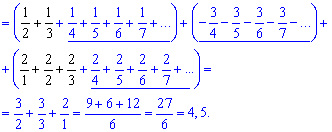

Сумма ряда равна 4,5 .

Пример 1.25 Вычислить сумму рядов:
а)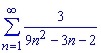


Поскольку она равна нулю то ряд сходится. Можем найти сумму ряда. Для этого по схеме предыдущих примеров раскладываем общий член ряда через простейшие дроби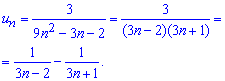

Это позволяет записать ряд через сумму простых рядов и, выделив в нем слагаемые, упростив при этом суммирование.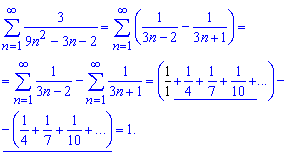

В этом случае останется одно слагаемое которое равен единице.
б)
Вычисления: Находим границу общего члена ряда

и убеждаемся что ряд сходится. Далее общий член числового ряда методом неопределенных коэффициентов раскладываем на дроби простейшего типа.

Через такие же дроби расписываем сумму ряда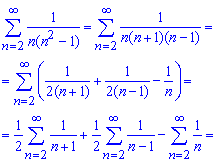

Записываем ряды в явном виде и упрощаем к сумме 3 слагаемых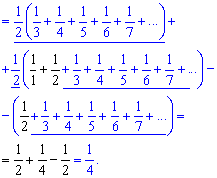

Сумма ряда равна 1/4.
На этом ознакомление со схемами суммирования рядов завершено. Здесь еще не рассмотрены ряды, которые сводятся к сумме бесконечно убывающей геометрической прогрессии, содержащие факториалы, степенные зависимости и подобные. Однако и приведенный материал будет полезен для студентов на контрольных и тестах.

4. Что такое a, b, c в выражении a + b = c? 5. Что значит найти сумму чисел a и b? 6. Если слагаемые в сумме переставить, сумма изменится? 7. Как читается коммутативный закон сложения? 8. Как читается ассоциативный закон сложения? 9. Можно ли переставлять слагаемые и заключать их в скобки? 10. Для чего используют законы сложения? Задание 5. Поставьте вместо точек подходящие по смыслу прила- гательные. 1. От перестановки слагаемых сумма не меняется – это … закон сложения. 2. Чтобы к сумме двух чисел прибавить третье число, можно к первому числу прибавить сумму второго и третьего – это … закон сложения. 3. 2 + 3 = 3 + 2 = 5 – это пример … закона сложения. 4. (2 + 3) + 4 = 2 + (3 + 4) = 9 – это пример … Запомните! Чтобы Можно + инфинитив (цель – зачем?) Нужно Задание 6. Поставьте глаголы в скобках в нужной форме. 1. Арифметика (изучать) действия над числами. 2. Слагаемые в сумме можно (переставить). 3. При этом сумма не (измениться). 4. От перестановки слагаемых сумма не (изменяться). 5. Чтобы к сумме двух чисел (прибавить) третье число, можно к первому числу (прибавить) сумму второго и третьего. 6. В сумме нескольких слагаемых можно (переставлять) слагае- мые и (заключать) их в скобки любым способом. 7. Законы сложения используют, чтобы (упростить) вычисления. Задание 7. Прочитайте выражения по модели. М о д е л ь: a + b = c ⇒ выражение a плюс b будет c – это сложе- ние, где a – это слагаемое, b – это слагаемое, c – это сумма (результат), a + b – это тоже сумма. 5+3=8 100 + 6 = 106 200 + 14 = 214 6 + 4 = 10 17 + 4 = 21 13 + 184 = 197 14 + 4 = 18 38 + 4 = 42 81 + 3 = 84 30 + 5 = 35 99 + 1 = 100 65 + 10 = 75 21 Задание 8. Задайте вопрос по модели и решите примеры. М о д е л ь: – Сколько будет (получится) 25 + 5? – 25 + 5 будет (получится) 30. 33 + 6 = 68 + 10 = 13 + 13 = 76 + 4 = 48 + 2 = 11 + 11 = 97 + 3 = 89 + 15 = 99 + 14 = 19 + 12 = 170 + 14 = 53 + 10 = 39 + 1 = 9 + 10 = 19 + 31 = 77 + 77 = Задание 9. Закончите предложения. 1. Арифметика изучает … 2. a + b = c – это … 3. Плюс – это … 4. a и b – это … 5. c – это … 6. Найти сумму чисел a и b – это … 7. Слагаемые в сумме … 8. От перестановки слагаемых … 9. Чтобы к сумме двух чисел прибавить третье число … 10. В сумме нескольких слагаемых можно … 11. Законы сложения используют, чтобы … 22 Занятие 6 АРИФМЕТИЧЕСКИЕ ДЕЙСТВИЯ. ВЫЧИТАНИЕ СЛОВА И СЛОВОСОЧЕТАНИЯ Вычитаемое (сущ., ср.р.) Вычитание Вычитание – это действие Выполнить вычитание Вычитать I, вычесть I Вычитать числа (вычту, вычтешь) (что?) вычесть (из чего?) Число 2 вычесть из числа 7 Показывать I, показать I (что?) Разность (ж.р.) Разность чисел Найти разность чисел На сколько На сколько число 5 больше числа 2? Уменьшаемое (сущ., ср.р.) ТЕКСТ ДЛЯ ЧТЕНИЯ Арифметика изучает действия с числами. Пусть a и b – натуральные числа. Пусть a ≥ b. Разность чисел a и b – это число c = a – b. Сумма этого числа с числом b равна числу a, т.е. (a – b) + b = a. a – b = c – это вычитание. (a минус b равно числу с) Вычитание – это действие. – (минус) – это знак действия вычитания, a – это уменьшаемое, b – это вычитаемое, c – это разность, a – b – это тоже разность. a и b – это компоненты действия вычитания, c (разность) – это ре- зультат действия вычитания. Запись 12 – 5 = 7 читаем так: «12 минус 5 равно числу семь». Найти разность чисел a и b – это значит вычесть из числа a число b. Разность двух чисел показывает, на сколько одно число больше (или меньше), чем другое число. Например, 12 > 5 на 7, потому что 12 – 5 = 7. Чтобы определить, на сколько одно число больше (или меньше), чем другое число, надо найти разность этих чисел. 23 ЗАДАНИЯ Задание 1. Прочитайте слова и словосочетания и переведите не- знакомые по словарю. Задание 2. Образуйте существительные от глаголов. М о д е л ь: слагать – слагаемое. Вычитать – …, уменьшать –…, изучать – …. Задание 3. Сгруппируйте однокоренные слова: вычитать, слагать, уменьшать, слагаемое, уменьшение, вычитание, разность, вычитаемое, сложение, уменьшаемое, разный, вычесть, разница. Задание 4. Прочитайте текст и ответьте на вопросы. 1. Какой знак обозначает разность? 2. Что такое вычитание? 3. Что такое a, b, c в выражении a – b = c? 4. Что значит найти разность чисел a и b? 5. Что показывает разность чисел? 6. Что нужно сделать, чтобы определить, на сколько одно число больше (или меньше), чем другое число? Задание 5. Прочитайте выражения по модели. М о д е л ь: a – b = c ⇒ выражение a минус b будет c – это вычи- тание, где a – это уменьшаемое; b – это вычитаемое; c – это разность (результат), a – b – это тоже разность. 8–5=3 c–d=x 130 – 30 = 100 16 – 1 = 15 y–x=z 201 – 3 = 198 19 – 3 = 16 12a – 3b = 4c 300 – 4 = 296 100 – 1 = 99 3d – 2c = x 1000 – 100 = 900 Запомните! Что? больше, чем что? на сколько? (меньше) 5 больше, чем 3, на 2 Задание 6. Сравните числа по модели. М о д е л ь: 9 > 5 на 4, потому что 9 – 5 = 4. 90 и 80; 13 и 25; 18 и 3; 16 и 17; 20 и 2; 15 и 20; 200 и 190; 7 и 4; 38 и 30; 40 и 38; 12 и 19; 123 и 123; 123 и 124; 123 и 121; 12 345 и 12 346; 75 315 и 75 515; 101 001 и 100 101. Задание 7. а) Ответьте на вопросы. 1. Что показывает разность? 2. На сколько число 12 больше, чем число 9? 24 3. На сколько число 9 меньше, чем число 12? 4. На сколько число 50 больше, чем число 30, а 30 меньше, чем 50? 5. На сколько число 19 больше, чем число 12, а 12 меньше, чем 19? 6. На сколько 29 > 19? 7. На сколько 11 < 20? б) Задайте друг другу вопросы по модели. М о д е л ь: что? больше (меньше), чем что?, на сколько? Запомните! Что? вычесть из чего? Число 2 вычесть из числа 5 Задание 8. Прочитайте выражения по модели и назовите результат. М о д е л ь: 12 – 6 = 6 ⇒ число 6 вычесть из числа 12 будет 6. 13 – 6 = 16 – 1 = 10 – 9 = 17 – 4 = 100 – 13 = 15 – 3 = 10 – 1 = 14 – 11 = 60 – 10 = 33 – 2 = 19 – 12 = 74 – 5 = 25 Занятие 7 АРИФМЕТИЧЕСКИЕ ДЕЙСТВИЯ. УМНОЖЕНИЕ СЛОВА И СЛОВОСОЧЕТАНИЯ Выносить II, вынести I Множитель вынести за скобки (что? куда?) Вынесение (чего? куда?) Вынесение множителя за скобки Закон Дистрибутивный закон умножения Множитель (м.р.) Общий множитель Произведение (чего?) Произведение множителей Найти произведение чисел Раскрывать I, раскрыть I Раскрыть скобки (что?) Способ Умножать I, умножить II Число 2 умножить на число 5 (что? на что?) Умножать (что?) Умножать числа Умножение (чего?) Умножение чисел Выполнить умножение ТЕКСТ ДЛЯ ЧТЕНИЯ Арифметика изучает действия с числами. Пусть a и b – натуральные числа. a · b = c (или a Ч b = c) – это умножение. (a умножить на b равно числу с) Умножение – это действие. · или Ч (умножить) – это знаки действия умножения, a – это мно- житель, b – это множитель, a и b – это множители, c – это произведе- ние, a · b – это тоже произведение. a и b – это компоненты действия умножения, c (произведение) – это результат действия умножения. Запись 12 · 5 = 60 читаем так: «12 умножить на 5 равно числу шестьдесят». Найти произведение чисел a и b – это значит умножить число a на число b. Запомните коммутативный закон умножения! От перестановки множителей произведение не изменяется, т.е. для любых натуральных чисел a и b верно равенство: a · b = b · a. 26 Запомните ассоциативный закон умножения! Чтобы произведение двух чисел умножить на третье число, мож- но первое число умножить на произведение второго и третьего чисел, т.е. для любых натуральных чисел a, b и с верно равенство: (a · b) · c = a · (b · c). В произведении нескольких множителей можно переставлять множители и заключать их в скобки любым способом. Для любого неотрицательного числа верны равенства: a · 0 = 0; 0 · a = 0; a · 1 = a; 1 · a = a. Запомните дистрибутивный закон умножения! Чтобы число умножить на сумму двух чисел, можно это число умножить на каждое слагаемое и полученные произведения сложить, т.е. для любых натуральных чисел a, b и с верно равенство: a · (b + c) = a · b + a · c. Дистрибутивный закон можно записать для любого числа слагае- мых. Например, верно равенство: a · (b + c + d) = a · b + a · c + a · d. Законы умножения используют, чтобы упростить вычисления. Например, 95 · 43 + 95 · 57 = 95 · (43 + 57) = 95 · 100 = 9500. Переход от a · b + a · c к a · (b + c) – это вынесение общего мно- жителя за скобки. Выполнить переход от a · b + a · c к a · (b + c) – значит вынести общий множитель за скобки. Переход от a · (b + c) к a · b + a · c – это раскрытие скобок. Вы- полнить переход от a · (b + c) к a · b + a · c – значит раскрыть скобки. ЗАДАНИЯ Задание 1. Прочитайте слова и словосочетания и переведите не- знакомые по словарю. Задание 2. Образуйте существительные от глаголов при помощи суффикса -ени- по модели. М о д е л ь: сложить – сложение. Перенести – …, делить – …, умножить – …, вычислить – …, про- извести (ст – д) – …, упростить (ст – щ) – …, вынести – … Задание 3. Прочитайте текст и ответьте на вопросы. 1. Какой знак обозначает произведение? 2. Что такое a, b, c в выражении a · b = c? 27 3. Что значит найти произведение чисел a и b? 4. Как читается коммутативный закон умножения? 5. Как читается ассоциативный закон умножения? 6. Что считают по определению? 7. Как читается дистрибутивный закон умножения? 8. Для чего используют законы умножения? 9. Что такое переход от a · b + a · c к a · (b + c)? 10. Что такое раскрытие скобок? 11. Что значит выполнить переход от a·(b + c) к a · b + a · c? Задание 4. Закончите предложения. 1. Коммутативный за- а) чтобы произведение двух чисел ум- кон умножения: ножить на третье число, можно первое число умножить на произведение второ- го и третьего чисел. 2. Дистрибутивный б) можно переставлять множители и закон умножения: заключать их в скобки любым спосо- бом. 3. Ассоциативный за- в) чтобы число умножить на сумму двух кон умножения: чисел, можно это число умножить на каждое слагаемое и полученные произ- ведения сложить. 4. В произведении не- г) от перестановки множителей произ- скольких множителей… ведение не изменяется. Задание 5. Прочитайте выражения по модели. М о д е л ь: a · b = c ⇒ выражение a умножить на b будет c – это умножение, где a – это множитель; b – это множитель; c – это произ- ведение (результат), a · b – это тоже произведение. 12 · 3 = 36 40 · 3 = 120 12 · 4 = 48 33 · 3 = 99 14 · 2 = 28 18 · 2 = 36 100 · 10 = 1000 11 · 11 = 121 2·2=4 8 · 6 = 48 6 · 8 = 48 12 · 5 = 60 3 · 13 = 39 15 · 3 = 45 90 · 8 = 720 70 · 3 = 210 Запомните! Раскрыть скобки – раскрытие скобок Вынести множитель – вынесение множителя Умножать числа – умножение чисел законы умножения 28 Задание 6. Поставьте слова в скобках в нужной форме. 1. 12 (умножить) на 5 равно (число) 60. 2. Найти произведение (числа) a и b – это значит умножить чис- ло a на число b. 3. От перестановки множителей произведение не (изменяться). 4. Чтобы произведение двух чисел (умножить) на третье число, можно первое число (умножить) на произведение (второй) и (третий) чисел. 5. В произведении нескольких множителей можно переставлять (множитель) и заключать (они) в скобки любым способом. 6. Чтобы число умножить на (сумма) двух чисел, можно это чис- ло умножить на (каждый) слагаемое и (полученные) произведения сложить. Задание 7. Закончите предложения. 1. Найти произведение чисел a и b – значит … 2. Коммутативный закон умножения: … 3. Чтобы произведение двух чисел умножить на третье число, можно … 4. В произведении нескольких множителей можно … 5. По определению считают, что … 6. Чтобы число умножить на сумму двух чисел, можно … 7. Дистрибутивный закон можно … 8. Чтобы упростить вычисления, … 9. Переход от a · b+a · c к a · (b+c) – это … 10. Переход от a · (b+c) к a · b+a · c – это … 29 Занятие 8 АРИФМЕТИЧЕСКИЕ ДЕЙСТВИЯ. СТЕПЕНЬ С НАТУРАЛЬНЫМ ПОКАЗАТЕЛЕМ СЛОВА И СЛОВОСОЧЕТАНИЯ Возводить II, возвести I Возвести число в степень (что? во что?) Возведение (чего? во что?) Возведение числа в степень Основание (чего?) Основание степени Показатель (м.р.) (чего?) Показатель степени Степень (ж.р.) Натуральная степень Степень числа Число 2 в степени 5 Степень с натуральным показателем ТЕКСТ ДЛЯ ЧТЕНИЯ Сумму одинаковых слагаемых можно записать в виде произведе- ния: 5 + 5 + 5 + 5 = 4 · 5, a + a + a + a = 4 · a. В этом случае запись ста- новится короче. Произведение одинаковых множителей также можно записать ко- роче: 5 · 5 · 5 · 5 = 54, a · a · a = a3. Это степень. Читаем степени так: «пять в степени четыре», «a в степени три». Например, запись 23 – «два в степени три» – означает 2 · 2 · 2. Число 2 – это основание степени, число 3 – это показатель степени. Число 3 показывает, сколько раз нужно взять множителем основание – число 2: 23 = 2 · 2 · 2 = 8. Таким образом, степень числа a с натуральным показателем n (n > 1) – это произведение n множителей, каждый из которых равен a. a n = a ⋅ a ⋅ a ⋅ ... ⋅ a , n > 1 , 14 244 4 3 n где a n = b – это возведение в степень (a в степени n равно числу b). Возведение в степень – это действие. a – это основание степени, n – это показатель степени, b – это степень, a n – это тоже степень. Любое число в степени один равно самому числу, т.е. 21 = 2, 51 = 5, … , a1 = a. 30