Что можно приготовить из кальмаров: быстро и вкусно
1.Показательная функция – это функция вида у(х) =а х, зависящая от показателя степени х, при постоянном значении основания степени a , где а > 0, a ≠ 0, xϵR (R – множество действительных чисел).
Рассмотрим график функции, если основание не будет удовлетворять условию: а>0
a) a < 0
Если a < 0 – возможно возведение в целую степень или в рациональную степень с нечетным показателем.
а = -2

Если а = 0 – функция у = определена и имеет постоянное значение 0

в) а =1
Если а = 1 – функция у = определена и имеет постоянное значение 1
Область определения функции (ООФ) Область допустимых значений функции (ОДЗ) 3. Нули функции (у = 0) 4. Точки пересечения с осью ординат oy (x = 0) 5. Возрастания, убывания функции Если , то функция f(x) возрастает 6. Чётность, нечётность функции Функция у = не симметрична относительно оси 0у и относительно началу координат, следовательно не является ни чётной, ни нечётной. (Функция общего вида) 7. Функция у = экстремумов не имеет 8. Свойства степени с действительным показателем: Пусть а > 0; a≠1 Тогда для xϵR; yϵR: Свойства монотонности степени: если , то Если a> 0, , то . 9. Относительное расположение фунцкции Чем больше основание а, тем ближе к осям ох и оу a > 1, a = 20 Пример 1. Решение большинства математических задач так или иначе связано с преобразованием числовых, алгебраических или функциональных выражений. Сказанное в особенности относится к решению . В вариантах ЕГЭ по математике к такому типу задач относится, в частности, задача C3. Научиться решать задания C3 важно не только с целью успешной сдачи ЕГЭ, но и по той причине, что это умение пригодится при изучении курса математики в высшей школе. Выполняя задания C3, приходится решать различные виды уравнений и неравенств. Среди них — рациональные, иррациональные, показательные, логарифмические, тригонометрические, содержащие модули (абсолютные величины), а также комбинированные. В этой статье рассмотрены основные типы показательных уравнений и неравенств, а также различные методы их решений. О решении остальных видов уравнений и неравенств читайте в рубрике « » в статьях, посвященных методам решения задач C3 из вариантов ЕГЭ по математике. Прежде чем приступить к разбору конкретных показательных уравнений и неравенств
, как репетитор по математике, предлагаю вам освежить в памяти некоторый теоретический материал, который нам понадобится. Функцию вида y
= a x
, где a
> 0 и a
≠ 1, называют показательной функцией
. Основные свойства показательной функции
y
= a x
: Графиком показательной функции является экспонента
: Графики показательных функций (экспоненты) Показательными
называются уравнения, в которых неизвестная переменная находится только
в показателях каких-либо степеней. Для решения показательных уравнений
требуется знать и уметь использовать следующую несложную теорему: Теорема 1.
Показательное уравнение a
f
(x
) = a
g
(x
) (где a
> 0, a
≠ 1) равносильно уравнению f
(x
) = g
(x
). Помимо этого, полезно помнить об основных формулах и действиях со степенями: Title="Rendered by QuickLaTeX.com"> Пример 1.
Решите уравнение: Решение:
используем приведенные выше формулы и подстановку: Уравнение тогда принимает вид: Дискриминант полученного квадратного уравнения положителен: Title="Rendered by QuickLaTeX.com"> Это означает, что данное уравнение имеет два корня. Находим их: Переходя к обратной подстановке, получаем: Второе уравнение корней не имеет, поскольку показательная функция строго положительна на всей области определения. Решаем второе: С учетом сказанного в теореме 1 переходим к эквивалентному уравнению: x
= 3. Это и будет являться ответом к заданию. Ответ:
x
= 3. Пример 2.
Решите уравнение: Решение:
ограничений на область допустимых значений у уравнения нет, так как подкоренное выражение имеет смысл при любом значении x
(показательная функция y
= 9 4 -x
положительна и не равна нулю). Решаем уравнение путем равносильных преобразований с использованием правил умножения и деления степеней: Последний переход был осуществлен в соответствии с теоремой 1. Ответ:
x
= 6.
Пример 3.
Решите уравнение: Решение:
обе части исходного уравнения можно поделить на 0,2 x
. Данный переход будет являться равносильным, поскольку это выражение больше нуля при любом значении x
(показательная функция строго положительна на своей области определения). Тогда уравнение принимает вид: Ответ:
x
= 0. Пример 4.
Решите уравнение: Решение:
упрощаем уравнение до элементарного путем равносильных преобразований с использованием приведенных в начале статьи правил деления и умножения степеней: Деление обеих частей уравнения на 4 x
, как и в предыдущем примере, является равносильным преобразованием, поскольку данное выражение не равно нулю ни при каких значениях x
. Ответ:
x
= 0. Пример 5.
Решите уравнение: Решение:
функция y
= 3 x
, стоящая в левой части уравнения, является возрастающей. Функция y
= —x
-2/3, стоящая в правой части уравнения, является убывающей. Это означает, что если графики этих функций пересекаются, то не более чем в одной точке. В данном случае нетрудно догадаться, что графики пересекаются в точке x
= -1. Других корней не будет. Ответ:
x
= -1. Пример 6.
Решите уравнение: Решение:
упрощаем уравнение путем равносильных преобразований, имея в виду везде, что показательная функция строго больше нуля при любом значении x
и используя правила вычисления произведения и частного степеней, приведенные в начале статьи: Ответ:
x
= 2. Показательными
называются неравенства, в которых неизвестная переменная содержится только
в показателях каких-либо степеней. Для решения показательных неравенств
требуется знание следующей теоремы: Теорема 2.
Если a
> 1, то неравенство a
f
(x
) > a
g
(x
) равносильно неравенству того же смысла: f
(x
) > g
(x
). Если 0 < a
< 1, то показательное неравенство a
f
(x
) > a
g
(x
) равносильно неравенству противоположного смысла: f
(x
) < g
(x
). Пример 7.
Решите неравенство: Решение:
представим исходное неравенство в виде: Разделим обе части этого неравенства на 3 2x
, при этом (в силу положительности функции y
= 3 2x
) знак неравенства не изменится: Воспользуемся подстановкой: Тогда неравенство примет вид: Итак, решением неравенства является промежуток: переходя к обратной подстановке, получаем: Левое неравенства в силу положительности показательной функции выполняется автоматически. Воспользовавшись известным свойством логарифма, переходим к эквивалентному неравенству: Поскольку в основании степени стоит число, большее единицы, эквивалентным (по теореме 2) будет переход к следующему неравенству: Итак, окончательно получаем ответ:
Пример 8.
Решите неравенство: Решение:
используя свойства умножения и деления степеней, перепишем неравенство в виде: Введем новую переменную: С учетом этой подстановки неравенство принимает вид: Умножим числитель и знаменатель дроби на 7, получаем следующее равносильное неравенство: Итак, неравенству удовлетворяют следующие значения переменной t
: Тогда, переходя к обратной подстановке, получаем: Поскольку основание степени здесь больше единицы, равносильным (по теореме 2) будет переход к неравенству: Окончательно получаем ответ:
Пример 9.
Решите неравенство: Решение:
Делим обе части неравенства на выражение: Оно всегда больше нуля (из-за положительности показательной функции), поэтому знак неравенства изменять не нужно. Получаем: t
, находящиеся в промежутке: Переходя к обратной подстановке получаем, что исходное неравенство распадается на два случая: Первое неравенство решений не имеет в силу положительности показательной функции. Решаем второе: Пример 10.
Решите неравенство: Решение:
Ветви параболы y
= 2x
+2-x
2 направлены вниз, следовательно она ограничена сверху значением, которое она достигает в своей вершине: Ветви параболы y
= x
2 -2x
+2, стоящей в показателе, направлены вверх, значит она ограничена снизу значением, которое она достигает в своей вершине: Вместе с этим ограниченной снизу оказывается и функция y
= 3 x
2 -2x
+2 , стоящая в правой части уравнения. Она достигает своего наименьшего значения в той же точке, что и парабола, стоящая в показателе, и это значение равно 3 1 = 3. Итак, исходное неравенство может оказаться верным только в том случае, если функция слева и функция справа принимают в одной точке значение, равное 3 (пересечением областей значений этих функций является только это число). Это условие выполняется в единственной точке x
= 1. Ответ:
x
= 1. Для того, чтобы научиться решать показательные уравнения и неравенства,
необходимо постоянно тренироваться в их решении. В этом нелегком деле вам могут помочь различные методические пособия, задачники по элементарной математике, сборники конкурсных задач, занятия по математике в школе, а также индивидуальные занятия с профессиональным репетитором. Искренне желаю вам успехов в подготовке и блестящих результатов на экзамене. P. S. Уважаемые гости! Пожалуйста, не пишите в комментариях заявки на решение ваших уравнений. К сожалению, на это у меня совершенно нет времени. Такие сообщения будут удалены. Пожалуйста, ознакомьтесь со статьёй. Возможно, в ней вы найдёте ответы на вопросы, которые не позволили вам решить своё задание самостоятельно. Концентрация внимания:
Определение. Функция
вида называется показательной
функцией
. Замечание. Исключение из числа значений
основания a
чисел 0; 1 и отрицательных значений a
объясняется следующими обстоятельствами: Само аналитическое выражение a x
в
указанных случаях сохраняет смысл и может
встречаться в решении задач. Например, для
выражения x y
точка x = 1; y
= 1
входит
в область допустимых значений. Построить графики функций: и . Свойства показательной функции Когда заполняется таблица, то параллельно с
заполнением решаются задания. Задание № 1. (Для нахождения области
определения функции). Какие значения аргумента являются допустимыми для функций: Задание № 2. (Для нахождения области
значений функции). На рисунке изображен график функции. Укажите
область определения и область значений функции: Задание № 3. (Для указания промежутков
сравнения с единицей). Каждую из следующих степеней сравните с
единицей: Задание № 4. (Для исследования функции на
монотонность). Сравнить по величине действительные числа m
и n
если: Задание № 5. (Для исследования функции на
монотонность). Сделайте заключение относительно основания a
,
если: y(x) = 10 x ; f(x) = 6 x ; z(x) - 4 x
Как располагаются графики показательных
функций относительно друг друга при x > 0, x = 0, x <
0? В одной координатной плоскости построены
графики функций: y(x) = (0,1) x ; f(x) = (0,5) x ; z(x) = (0,8) x .
Как располагаются графики показательных
функций относительно друг друга при x > 0, x = 0, x <
0? Число e
играет особую роль в математическом анализе. Показательная
функция
с основанием e
, называется
экспонентой
и обозначается y = e x
. Первые знаки числа
e
запомнить
несложно: два, запятая, семь, год рождения
Льва Толстого - два раза, сорок пять, девяносто,
сорок пять.
Домашнее задание: Колмогоров п. 35; № 445-447; 451; 453. Повторить алгоритм построения графиков
функций, содержащих переменную под знаком
модуля. Введем сначала определение показательной функции. Показательная функция $f\left(x\right)=a^x$, где $a >1$. Введем свойства показательной функции, при $a >1$.
\ \[корней\ нет.\] \ Пересечение с осями координат. Функция не пересекает ось $Ox$, но пересекает ось $Oy$ в точке $(0,1)$. $f""\left(x\right)={\left(a^xlna\right)}"=a^x{ln}^2a$
\ \[корней\ нет.\] \ График (рис. 1). Рисунок 1. График функции $f\left(x\right)=a^x,\ при\ a >1$.
Введем свойства показательной функции, при $0 Область определения -- все действительные числа. $f\left(-x\right)=a^{-x}=\frac{1}{a^x}$ -- функция ни четна, ни нечетна. $f(x)$ - непрерывна на всей области определения. Область значения -- интервал $(0,+\infty)$. $f"(x)=\left(a^x\right)"=a^xlna$
\ \[корней\ нет.\] \ \[корней\ нет.\] \ Функция выпукла на всей области определения. Поведение на концах области определения:
\[{\mathop{lim}_{x\to -\infty } a^x\ }=+\infty \] \[{\mathop{lim}_{x\to +\infty } a^x\ }=0\] График (рис. 2). Исследовать и построить график функции $y=2^x+3$. Решение.
Проведем исследование по примеру схемы выше: Область определения -- все действительные числа. $f\left(-x\right)=2^{-x}+3$ -- функция ни четна, ни нечетна. $f(x)$ - непрерывна на всей области определения. Область значения -- интервал $(3,+\infty)$. $f"\left(x\right)={\left(2^x+3\right)}"=2^xln2>0$ Функция возрастает на всей области определения. $f(x)\ge 0$ на всей области определения. Пересечение с осями координат. Функция не пересекает ось $Ox$, но пересекает ось $Oy$ в точке ($0,4)$ $f""\left(x\right)={\left(2^xln2\right)}"=2^x{ln}^22>0$ Функция выпукла на всей области определения. Поведение на концах области определения:
\[{\mathop{lim}_{x\to -\infty } a^x\ }=0\] \[{\mathop{lim}_{x\to +\infty } a^x\ }=+\infty \] График (рис. 3). Рисунок 3. График функции $f\left(x\right)=2^x+3$

2. Рассмотрим подробнее показательную функцию:
0


Если , то функция f(x) убывает
Функция y= , при 0
Это следует из свойств монотонности степени с действительным показателем.
b> 0; b≠1
Например:


Показательная функция непрерывна в любой точке ϵ R.


Если а0, то показательная функция принимает вид близкий к y = 0.
Если а1, то дальше от осей ох и оу и график принимает вид близкий к функции у = 1.
Построить график у =
Показательная функция
Что такое показательная функция?
График показательной функции
Решение показательных уравнений

![]()

![]()
![]()
![]()
![]()
Решение показательных неравенств

![]()

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

![]()
![]()
Сергей Валерьевич
График показательной функции
y =
a x
, a > 1
y =
a x
, 0< a < 1
Свойства показательной функции
y =
a x
, a > 1
y =
a x
, 0< a <
1
2. Область значений функции
3.Промежутки сравнения с
единицей
при x
> 0, a x
>
1
при x
> 0, 0< a x
< 1
при x
< 0, 0< a x
< 1
при x
< 0, a x
>
1
4. Чётность, нечётность.
Функция не является ни
чётной, ни нечётной (функция общего вида).
5.Монотонность.
монотонно возрастает на R
монотонно убывает на R
6. Экстремумы.
Показательная функция
экстремумов не имеет.
7.Асимптота
Ось O x
является
горизонтальной асимптотой.
8. При любых действительных
значениях x
и y
;
Число
одна из важнейших постоянных в математике. По
определению, оно равно пределу
последовательности
при
неограниченном
возрастании n
.
Обозначение e
ввёл Леонард Эйлер
в 1736 г. Он вычислил первые 23 знака этого числа в
десятичной записи, а само число назвали в честь
Непера «неперовым числом».
Показательная функция $f\left(x\right)=a^x$, где $0
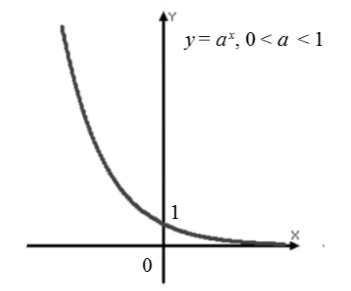
Пример задачи на построение показательной функции
