Что можно приготовить из кальмаров: быстро и вкусно
Теорема 1. Площадь трапеции равна произведению полусуммы ее оснований на высоту:
Теорема 2.
Диагонали трапеции делят ее на четыре треугольника, два из которых подобны, а два другие имеют одинаковую площадь:
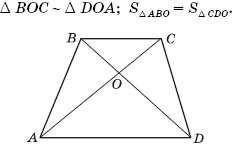
Теорема 3.
Площадь параллелограмма равна произведению основания на высоту, опущенную на данное основание, или произведению двух сторон на синус угла между ними: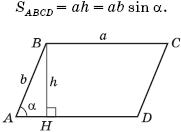
Иконки для создания прямоугольных и круговых паттернов. На чистом листе нарисуйте небольшой кусочек вокруг центра листа. Направьте нарисованный элемент - прямоугольная или круговая пиктограмма будет активирована. Щелкните значок прямоугольного шаблона. Появится ленточный бар, где значения по умолчанию уже находятся в поле редактирования отдельных параметров. Обратите внимание, что шаблон просматривается на экране. Попробуйте ввести разные значения в каждое поле редактирования в ленточном баре и посмотреть, как изменяется предварительный просмотр.
Теорема 4.
В параллелограмме сумма квадратов диагоналей равна сумме квадратов его сторон: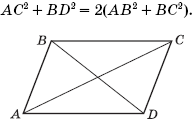
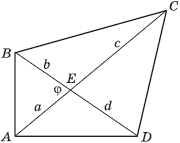
Теорема 5. Площадь произвольного выпуклого четырехугольника равна половине произведения его диагоналей на синус угла между ними:

Выбор первого приводит к тому, что шаблон определяется, указывая количество строк и столбцов и интервал между ними. Таким образом, размер шаблона является результатом. Когда вы выбираете второй вариант, вы определяете размер области, занимаемой шаблоном. Следовательно, с заданным количеством строк и столбцов результат между ними. В левом нижнем углу окна отображается список и кнопки для определения того, должны ли строки или столбцы перемещаться относительно друг друга, и если да, то какое должно быть значение смещения.
Попробуйте поэкспериментировать с этими параметрами - справа отображается предварительный просмотр. Отмените последнее действие так, чтобы на главном экране оставался только главный элемент. Вы увидите динамически меняющийся предварительный просмотр мыши. Нажмите на панели ленты значок «Параметры шаблона» и ознакомьтесь с окном - вы можете изменить параметры. Закройте окно параметров и создайте шаблон.
Теорема 6.
Площадь четырехугольника, описанного около окружности, равна произведению полупериметра этого четырехугольника на радиус данной окружности:
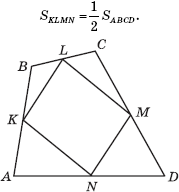
Теорема 7. Четырехугольник, вершинами которого являются середины сторон произвольного выпуклого четырехугольника, есть параллелограмм, площадь которого равна половине площади исходного четырехугольника:
Количество элементов в шаблоне и их интервал не имеют значения - важно только, чтобы элементы составляли не менее 3 или. Попробуйте указать любой элемент шаблона. Если выделены все элементы, в инструменте выбора выбирается опция «Группа». Чтобы указать один элемент шаблона, щелкните значок «Один» в ленте инструмента выделения.
Вы заметите, что изменение одного элемента в шаблоне не влияет на остальных. Однако это относится только к проекту модуля - в пространстве другое. Перемещение и копирование, поворот, зеркальное отображение. Нарисуйте вертикальную секцию и круг. Нажмите значок «Переместить». Программа попросит вас указать элементы, которые необходимо изменить. Когда элементы закончены, программа запрашивает базовую точку смещения. Базовая точка следует понимать как начало вектора смещения. Если вы хотите переместить объект по заданному значению, вы можете указать любую точку чертежа в качестве базовой точки - это не имеет значения, так как смещение вектора определяется координатами вектора.
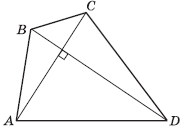
Теорема 8. Если у выпуклого четырехугольника диагонали взаимно перпендикулярны, то суммы квадратов противоположных сторон этого четырехугольника равны:
AB2 + CD2 = BC2 + AD2 .
Статья опубликована при поддержке компании "ДКРОСТ". Горки детские , домики, песочницы и многое другое - изготовление и продажа детских площадок оптом и в розницу. Самые низкие цены, скидки, сжатые сроки изготовления, выезд и консультация специалиста, гарантия качества. Узнать подробнее о компании, посмотреть каталог товаров, цены и контакты Вы сможете на сайте, который располагается по адресу: http://dkrost.ru/.
Случай отличается, если вы ищете конкретный пункт назначения, например, вы хотите переместить круг таким образом, чтобы он находился в середине раздела. В этом случае базовая точка будет центром круга, а центральная точка будет центром сегмента. Обратите внимание на значок «Копировать» - первый в левой панели ленты. Когда он выключен, объект перемещается, когда он включен. Это относится ко всем командам в этой группе, за исключением растягивания.
В ленточном баре есть три поля редактирования. Как вы можете видеть, определение смещения может быть выполнено двумя способами: с помощью мыши или ввода значения смещения в панели ленты. В последнем случае, однако, вы должны указать страницу смещения. Перемещение и копирование элементов на чертеже может быть еще одним способом: перетаскивание мыши. Вы уже использовали этот метод в упражнениях отношения. Этот метод выполняется быстрее, но его недостатком является то, что невозможно точно определить смещение.
Доказательства некоторых теорем
Доказательство теоремы 2 . Пусть ABCD - данная трапеция, AD и BC - ее основания, O - точка пересечения диагоналей AC и BD этой трапеции. Докажем, что треугольники AOB и COD имеют одинаковую площадь. Для этого опустим из точек B и C на прямую AD перпендикуляры BP и CQ. Тогда площадь треугольника ABD равна
Он подходит только для приблизительного расположения элементов на чертеже. Нажмите значок другой команды из этой группы: Повернуть. Как и прежде, программа будет запрашивать элементы для изменения. Обратите внимание на значок «Копировать» в панели ленты. Настройки по умолчанию для этого значка различны для разных команд этой группы, поэтому всегда проверяйте, включено ли оно или нет.
Как только элементы будут указаны, программа попросит вас указать центр вращения. Теперь программа запрашивает начальную точку поворота. Отправной точкой поворота является точка, определяющая первое плечо - это будет линия, проходящая через центр вращения, и это точка. Последнее слово, запрошенное программой, является конечной точкой вращения. Он определяется как точка начала вращения - путем нажатия на выбранную точку или объект. Вы также можете ввести значение угла поворота в полосе ленты. В таком случае вам придется - как и смещение - указать страницу вращения.
![]()
А площадь треугольника ACD равна ![]()
Так как BP = CQ, то и S∆ABD = S∆ACD . Но площадь треугольника AOB есть разность площадей треугольников ABD и AOD, а площадь треугольника COD - разность площадей треугольников ACD и AOD. Следовательно, площади треугольников AOB и COD равны, что и требовалось доказать.
Одна из полосок ленточного пояса - возможно, несколько неоднозначная - это название Угол положения. Это просто угол наклона линии, соединяющей курсор с центром вращения. Конечно, угол обзора изменяется при перемещении мыши. Вероятно, вы заметили сходство между определением смещения и поворота. В любом случае это можно сделать с помощью мыши или со значениями в полосе ленты.
Центр вращения и начальная точка должны быть указаны как на рисунке, а для определения угла поворота установите курсор так, чтобы рядом с ним появился знак отношения уровня. Многоугольник, имеющий четыре стороны, называется четырехугольником. Сумма квадратичных углов равна 360 °.
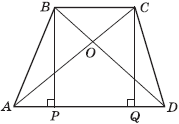
Доказательство теоремы 4
. Пусть ABCD - параллелограмм, AB = CD = a
, AD = BC = b,
AC = d1
, BD = d2
, ∠BAD = α, ∠ADC = 180° – α. Применим к треугольнику ABD теорему косинусов:
Применив теперь теорему косинусов к треугольнику ACD, получим:
Складывая почленно полученные равенства, получаем, что ![]() что и требовалось доказать.
что и требовалось доказать.
Трапез - это четырехугольник с по меньшей мере одной парой параллельных сторон. В равнобедренной трапеции углы у основания равны. 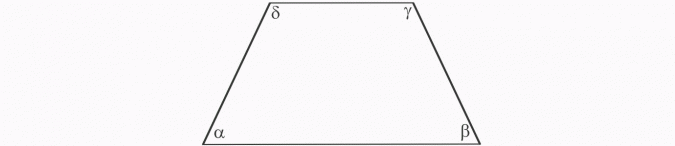
В трапеции сумма углов углов, лежащих на одной руке, составляет 180 °. Параллелограмм - это четырехугольник, имеющий две пары параллельных сторон.
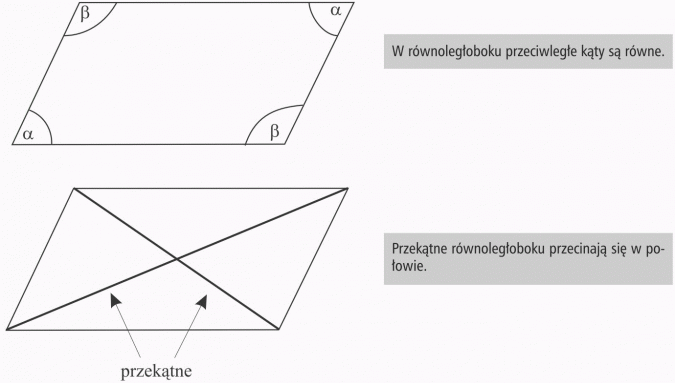
Алмаз - это параллелограмм, имеющий стороны равной длины. 
Диагональные алмазы пересекаются пополам и перпендикулярны. 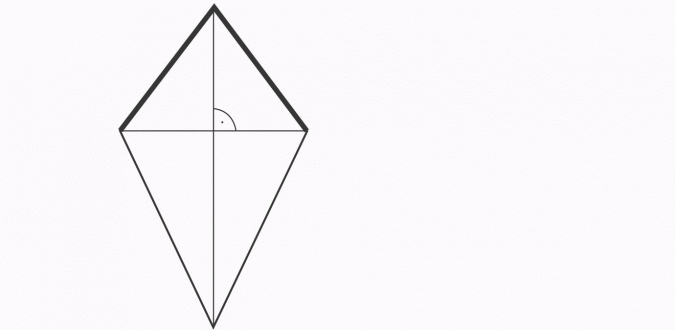
В диагональных диагоналях они пересекаются под прямым углом, а одна диагонально делит другую на половину. Прямоугольник - прямоугольник, который имеет все прямые углы.

Доказательство теоремы 5. Пусть ABCD - произвольный выпуклый четырехугольник, E - точка пересечения его диагоналей, AE = a
, BE = b,
CE = c, DE = d, ∠AEB = ∠CED = ϕ, ∠BEC =
= ∠AED = 180° – ϕ. Имеем:
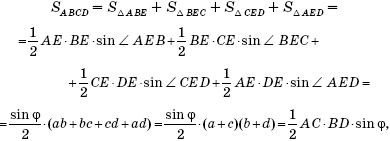
что и требовалось доказать.

Диагональные прямоугольники равны и пересекаются пополам. Квадрат - это четырехугольник, который имеет все стороны и прямые углы. 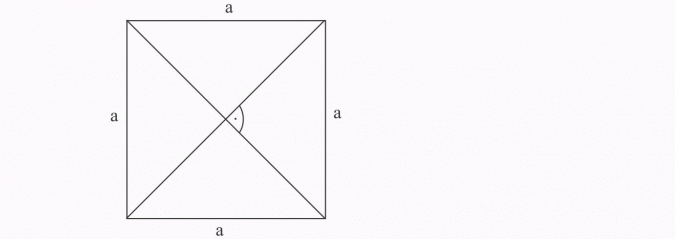
Диагональные квадраты равны, делятся на половину и пересекаются под прямыми углами. Вычислить меру углов α, β, γ, δ в трапеции.

На рисунке показано, что это равнобедренная трапеция, поэтому углы у основания равны, поэтому. 
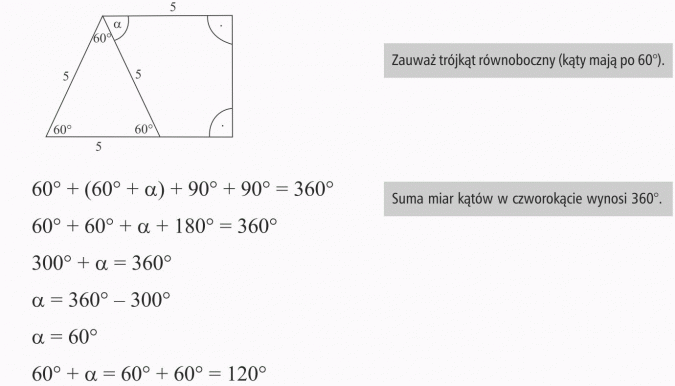
Область описывает объем пространства в пределах двумерного диапазона. Единицы измерения используются в математике, технике, медицине и других областях, например, при расчете клеток, атомов или диаметре кровеносных сосудов или сантехнических трубок. В географии измеряются географические единицы, такие как города, озера, государства. Районные единицы также используются для описания плотности населения: плотность населения рассчитывается по количеству людей в определенной области.
Доказательство теоремы 6
. Пусть ABCD - произвольный четырехугольник, описанный около окружности, O - центр этой окружности, OK, OL, OM и ON - перпендикуляры, опущенные из точки O на прямые AB, BC, CD и AD соответственно. Имеем: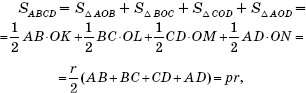
Квадратный метр - это область системного блока. Квадратный метр обозначает площадь квадрата, каждый с запасом 1 метр. Квадратный блок представляет собой квадрат, края которого равны определенной длине единицы. То есть квадрат квадрата равен единице. В декартовой системе координат координаты такого квадрата обычно расположены в и в двумерном пространстве.
Массив составляет 100 квадратных метров. Различные регионы имеют разные названия. Он обычно используется для измерения небольших участков, где гектар слишком велик. Гаты также измеряют землю. Гектары использовались до сих пор во Французской революции и в Европейском союзе. В большинстве стран встречаются местные гектары, причем только их имена различны.
где r - радиус окружности, а p - полупериметр четырехугольника ABCD.
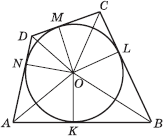
Доказательство теоремы 7 . Пусть ABCD - произвольный выпуклый четырехугольник, K, L, M и N - середины сторон AB, BC, CD и AD соответственно. Так как KL - средняя линия треугольника ABC, то прямая KL параллельна прямой AC и Аналогично, прямая MN параллельна прямой AC и Следовательно, KLMN - параллелограмм. Рассмотрим треугольник KBL. Его площадь равна четверти площади треугольника ABC. Площадь треугольника MDN также равна четверти площади треугольника ACD. Следовательно,
Площадь земельных площадей измеряется в Северной Америке и Бирме. Исторически, это область земли, в которой ярмо быков может сломаться за один день. В Барнау измеряется очень мало областей, таких как диаметр атомов в ядерной физике. Один сарай равен 10 -2 кв. Площадь приблизительно равна диаметру ядра урана; Физики шутя, ядро урана «большое, как сад».
Он появился во время Второй мировой войны, потому что ученым из Манхэттенского проекта было удобно использовать его в шифровании. Площадь не сложных объектов может быть рассчитана на основе квадрата, размер которого известен. Этот метод удобен, потому что площадь квадрата легко рассчитать. Это приводит к некоторым формулам для вычисления площади геометрических фигур. Площадь многоугольника рассчитывается путем деления многоугольника на треугольники и применения формул расчета треугольной области.
Аналогично, ![]()
Это значит, что
откуда вытекает, что ![]()

Доказательство теоремы 8
. Пусть ABCD - произвольный выпуклый четырехугольник, у которого диагонали взаимно перпендикулярны, пусть E - точка пересечения его диагоналей,
AE = a
, BE = b, CE = c, DE = d. Применим к треугольникам ABE и CDE теорему Пифагора:
AB2
= AE2
+ BE2
= a
2
+ b2
,
CD2
= CE2
+ DE2
= c2
+ d2
,
следовательно,
AB2
+ CD2
= a
2
+ b2
+ c2
+ d2
.
Применив теперь теорему Пифагора к треугольникам ADE и BCE, получим:
AD2
= AE2
+ DE2
= a
2
+ d2
,
BC2
= BE2
+ CE2
= b2
+ c2
,
откуда вытекает, что
AD2
+ BC2
= a
2
+ b2
+ c2
+ d2
.
Значит, AB2
+ CD2
= AD2
+ BC2
, что и требовалось доказать.
Расчет площади поверхности
Сложные цифры требуют сложных вычислений. Квадрат: его ограниченная область может быть найдена путем умножения ширины на ширину. Равный треугольник: квадратный корень из трех, разделенный на четыре и умноженный на квадрат квадрата. Эквивалентный градиент: ребра и высота продукта, опущенного к нему. сумма двух параллельных сторон, деленная на два и умноженная на высоту соединения этих ребер. Сфера: радиус квадрата и π-произведение. Эллипс: полуось и π-произведение.
- Квадрат: край, поднятый квадратом.
- Треугольник: половина края и высота продукта.
- Треугольник: половина произведения края, умноженное на угол синуса.

Решения задач
Задача 1 . Около круга описана трапеция с углами при основании α и β. Найти отношение площади трапеции к площади круга.

Решение . Пусть ABCD - данная трапеция, AB и CD - ее основания, DK и CM - перпендикуляры, опущенные из точек C и D на прямую AB. Искомое отношение не зависит от радиуса круга. Поэтому будем считать, что радиус равен 1. Тогда площадь круга равна π, найдем площадь трапеции. Так как треугольник ADK прямоугольный, то
![]()
Аналогично, из прямоугольного треугольника BCM находим, что Поскольку в данную трапецию можно вписать окружность, то суммы противоположных сторон равны:
AB + CD = AD + BC,
откуда находим
Значит, площадь трапеции есть
и искомое отношение равно ![]()
Ответ
: ![]()
Задача 2 . В выпуклом четырехугольнике ABCD угол A равен 90°, а угол C не превосходит 90°. Из вершин B и D на диагональ AC опущены перпендикуляры BE и DF. Известно, что AE = CF. Доказать, что угол C прямой.
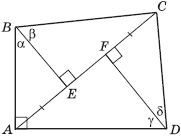
Доказательство
. Так как угол A равен 90°,
а угол C не превосходит 90°, то точки E и F лежат на диагонали AC. Без ограничения общности мы можем считать, что AE < AF (в противном случае следует повторить все нижеследующие рассуждения с заменой точек B и D). Пусть ∠ABE = α,
∠EBC = β, ∠FDA = γ, ∠FDC = δ. Нам достаточно доказать, что α + β + γ + δ = π. Так как


откуда получаем, что что и требовалось доказать.
Задача 3
. Периметр равнобочной трапеции, описанной около круга, равен p. Найти радиус этого круга, если известно, что острый угол при основании трапеции равен α.
Решение
. Пусть ABCD - данная равнобочная трапеция с основаниями AD и BC, пусть BH - высота этой трапеции, опущенная из вершины B.
Так как в данную трапецию можно вписать окружность, то ![]()
Следовательно,

Из прямоугольного треугольника ABH находим,
Ответ :
Задача 4 . Дана трапеция ABCD с основаниями AD и BC. Диагонали AC и BD пересекаются в точке O, а прямые AB и CD - в точке K. Прямая KO пересекает стороны BC и AD в точках M и N соответственно, а угол BAD равен 30°. Известно, что в трапеции ABMN и NMCD можно вписать окружность. Найти отношение площадей треугольника BKC и трапеции ABCD.
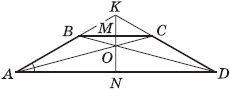
Решение
. Как известно, для произвольной трапеции прямая, соединяющая точку пересечения диагоналей и точку пересечения продолжений боковых сторон, делит каждое из оснований пополам. Итак, BM = MC и AN = ND. Далее, так как в трапеции ABMN и NMCD можно вписать окружность, то
BM + AN = AB + MN,
MC + ND = CD + MN.
Отсюда следует, что AB = CD, то есть трапеция ABCD - равнобокая. Искомое отношение площадей не зависит от масштаба, поэтому мы можем принять, что KN = x, KM = 1. Из прямоугольных треугольников AKN и BKM получаем, что Записывая вновь уже использованное выше соотношение
BM + AN = AB + MN ⇔
![]()
Нам требуется вычислить отношение:
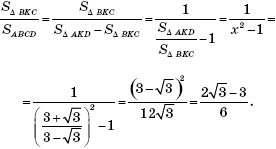
Здесь мы использовали тот факт, что площади треугольников AKD и BKC относятся как квадраты сторон KN и KM, то есть как x2.
Ответ:
Задача 5. В выпуклом четырехугольнике ABCD точки E, F, H, G являются серединами сторон AB, BC, CD, DA соответственно и O - точка пересечения отрезков EH и FG. Известно, что EH = a , FG = b, Найти длины диагоналей четырехугольника.. Пусть ABCD - данная трапеция, AB = 3 и CD = 5 - ее боковые стороны, точки K и M - середины сторон AB и CD соответственно. Пусть, для определенности, AD > BC, тогда площадь трапеции AKMD будет больше площади трапеции KBCM. Так как KM - средняя линия трапеции ABCD, то трапеции AKMD и KBCM имеют равные высоты. Поскольку площадь трапеции равна произведению полусуммы оснований на высоту, то верно следующее равенство:
![]()
Далее, так как в трапецию ABCD можно вписать окружность, то AD + BC = AB + CD = 8. Тогда KM = 4 как средняя линия трапеции ABCD. Пусть BC = x, тогда AD = 8 – x. Имеем: ![]()
Значит, BC = 1 и AD = 7.
Ответ: 1 и 7.
Задача 7 . Основание AB трапеции ABCD вдвое длиннее основания CD и вдвое длиннее боковой стороны AD. Длина диагонали AC равна a , а длина боковой стороны BC равна b. Найти площадь трапеции.
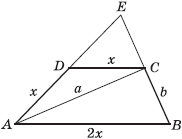
Решение . Пусть E - точка пересечения продолжений боковых сторон трапеции и CD = x, тогда AD = x, AB = 2x. Отрезок CD параллелен отрезку AB и вдвое его короче, значит, CD является средней линией треугольника ABE. Следовательно, CE = BC = b и DE = AD = x, откуда AE = 2x. Итак, треугольник ABE равнобедренный (AB = AE) и AC - его медиана. Поэтому AC является и высотой этого треугольника, и значит,
![]()
Так как треугольник DEC подобен треугольнику AEB с коэффициентом подобия то
AB + CD = 8. Продлим боковые стороны DA и CB до пересечения в точке E. Рассмотрим треугольник ABE, в котором ∠EAB = 50°. ∠EBA = 40°,
следовательно, ∠AEB = 90°. Медиана EM этого треугольника, проведенная из вершины прямого угла, равна половине гипотенузы: EM = AM. Пусть EM = x, тогда AM = x, DN = 4 – x. Согласно условию задачи MN = 1, следовательно,
EN = x + 1. Из подобия треугольников AEM и DEN имеем:
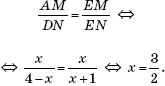
Это означает, что AB = 3 и CD = 5.
Ответ : 3 и 5.
Задача 10 . Выпуклый четырехугольник ABCD описан около окружности с центром в точке O, при этом AO = OC = 1, BO = OD = 2. Найти периметр четырехугольника ABCD.
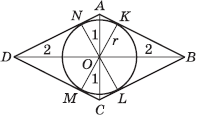
Решение . Пусть K, L, M, N - точки касания окружности со сторонами AB, BC, CD, DA соответственно, r - радиус окружности. Так как касательная к окружности перпендикулярна радиусу, проведенному в точку касания, то треугольники AKO, BKO, BLO, CLO, CMO, DMO, DNO, ANO - прямоугольные. Применив к этим треугольникам теорему Пифагора, получим, что
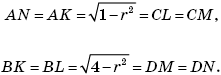
Следовательно, AB = BC = CD = DA, то есть ABCD - ромб. Диагонали ромба перпендикулярны друг другу, и точка их пересечения является центром вписанной окружности. Отсюда легко находим, что сторона ромба равна и значит, периметр ромба равен
Ответ :
Задачи для самостоятельного решения
С-1.
Около окружности радиуса r описана равнобочная трапеция ABCD. Пусть E и K - точки касания этой окружности с боковыми сторонами трапеции. Угол между основанием AB и боковой стороной AD трапеции равен 60°. Докажите, что EK параллелен AB, и найдите площадь трапеции ABEK.
С-2.
В трапеции диагонали равны 3 и 5, а отрезок, соединяющий середины оснований, равен 2.
Найдите площадь трапеции.
С-3
. Можно ли вокруг четырехугольника ABCD описать окружность, если ∠ADC = 30°, AB = 3, BC = 4, AC = 6?
С-4.
В трапеции ABCD (AB - основание) величины углов DAB, BCD, ADC, ABD и ADB образуют арифметическую прогрессию (в том порядке, в котором они написаны). Найдите расстояние от вершины C до диагонали BD, если высота трапеции равна h.
С-5.
Дана равнобедренная трапеция, в которую вписана окружность и около которой описана окружность. Отношение высоты трапеции к радиусу описанной окружности равно Найдите углы трапеции.
С-6.
Площадь прямоугольника ABCD равна 48, а длина диагонали равна 10. На плоскости, в которой расположен прямоугольник, выбрана точка O так, что OB = OD = 13. Найдите расстояние от точки O до наиболее удаленной от нее вершины прямоугольника.
С-7. Периметр параллелограмма ABCD равен 26. Величина угла ABC равна 120°. Радиус окружности, вписанной в треугольник BCD, равен Найдите длины сторон параллелограмма, если известно, что AD > AB.
С-8.
Четырехугольник ABCD вписан в окружность с центром в точке O. Радиус OA перпендикулярен радиусу OB, а радиус OC перпендикулярен радиусу OD. Длина перпендикуляра, опущенного из точки C на прямую AD, равна 9. Длина отрезка BC в два раза меньше длины отрезка AD. Найдите площадь треугольника AOB.
С-9.
В выпуклом четырехугольнике ABCD вершины A и C противоположны, а длина стороны AB равна 3. Угол ABC равен угол BCD равен Найдите длину стороны AD, если известно, что площадь четырехугольника равна ![]()
С-10.
В выпуклом четырехугольнике ABCD проведены диагонали AC и BD. Известно, что
AD = 2, ∠ABD = ∠ACD = 90°, и расстояние между точкой пересечения биссектрис треугольника ABD и точкой пересечения биссектрис треугольника ACD равно Найдите длину стороны BC.
С-11.
Пусть M - точка пересечения диагоналей выпуклого четырехугольника ABCD, в котором стороны AB, AD и BC равны между собой. Найдите угол CMD, если известно, что DM = MC,
а ∠CAB ≠ ∠DBA.
С-12.
В четырехугольнике ABCD известно, что ∠A = 74°, ∠D = 120°. Найдите угол между биссектрисами углов B и C.
С-13.
В четырехугольник ABCD можно вписать окружность. Пусть K - точка пересечения его диагоналей. Известно, что AB > BC > KC, а периметр и площадь треугольника BKC равны соответственно 14 и 7. Найдите DC.
С-14.
В трапеции, описанной около окружности, известно, что BC AD, AB = CD, ∠BAD =
= 45°. Найдите AB, если площадь трапеции ABCD равна 10.
С-15.
В трапеции ABCD с основаниями AB и CD известно, что ![]() ∠CAB = 2∠DBA. Найдите площадь трапеции.
∠CAB = 2∠DBA. Найдите площадь трапеции.
С-16.
В параллелограмме ABCD известно, что AC = a
, ∠CAB = 60°. Найдите площадь параллелограмма.
С-17
. В четырехугольнике ABCD диагонали AC и BD пересекаются в точке K. Точки L и M являются соответственно серединами сторон BC и AD. Отрезок LM содержит точку K. Четырехугольник ABCD таков, что в него можно вписать окружность. Найдите радиус этой окружности, если AB = 3, и LK: KM = 1: 3.
С-18.
В выпуклом четырехугольнике ABCD проведены диагонали AC и BD. При этом ∠BAC =
= ∠BDC, а площадь круга, описанного около треугольника BDC, равна
а) Найдите радиус окружности, описанной около треугольника ABC.
б) Зная, что BC = 3, AC = 4, ∠BAD = 90°, найдите площадь четырехугольника ABCD.
При решении планиметрических заданий курса геометрии нередко встречается фигура с 4-мя сторонами. Да, речь идет о четырехугольнике. Произвольный многоугольник с четырьмя углами встречается реже, чем его частные случаи, – трапеции, дельтоиды, параллелограммы. В последнюю «группу» входят также ромбы, прямоугольники, квадраты.
Рассмотрим, какие данные фигуры необходимо знать, чтобы рассчитать ее площадь.
Как найти площадь четырехугольника
Многоугольник произвольный
Для нахождения его площади вам потребуются диагонали фигуры, а также угол, полученный как результат их пересечения.
- S = (d1*d2*sinα)/2,
- d1, d2 – диагонали,
- α – угол, полученный путем их пересечения.
Многоугольник в окружности
Если заданный четырехугольник помещен в окружность, известна длина сторон фигуры, то в определении площади многоугольника поможет соотношение:
S = √(p – m)(p – k)(p – l)(p – e), p = (m + k + l + e)/2.
m, k, l, e – его стороны.

Как найти площадь четырехугольника — трапеции
Данную фигуру отличает наличие параллельных 2-ух сторон. Чтобы определить площадь такого многоугольника воспользуйтесь такими параметрами:
- Если известны величины параллельных сторон и перпендикуляра-высоты, проведенной к ним, площадь вычисляется с помощью выражения S = ((a + b)*h)/2,
a и b – основания,
h – перпендикуляр-высота. - Исходя из определения линии средины (k = (a + b)/2)), предыдущая формула приобретет следующий вид: S = k*h,
k – линия средины.
Известные диагонали трапеции и градусная мера угла, образованная в результате их пересечения, также помогут определить площадь фигуры: S = (d1*d2*sinβ)/2,
d1, d2 – диагонали,
β – угол, полученный путем их пересечения. - Заданы 4 стороны: S = ((m + l)√k 2 – ((m – l) 2 + k 2 – d 2) 2 /(4(m – l) 2))/2,
m, l — стороны параллельные,
k, d — стороны боковые.

Как найти площадь четырехугольника — дельтоида
Многоугольник-дельтоид характеризуется наличием 2-ух пар равных сторон. Вычислить площадь такого четырехугольника рассчитывается следующим образом:
- Известны стороны фигуры и угол, образованный сторонами разной длины:
S = m*l*sinϕ,
m, l – стороны дельтоида,
ϕ – угол между ними. - Известны стороны фигуры и углы, образованные сторонами равной длины:
S = m 2 *sinα/2 + l 2 *sinβ/2,
m, l – стороны дельтоида,
α, β — углы между равными сторонами. - Наличие известных диагоналей также позволяет определить площадь фигуры:
S = d1*d2/2,
d1, d2 – диагонали дельтоида. - Если в фигуру вписана окружность, то знание ее радиуса позволяет вычислить площадь дельтоида: S = (m + l)*r,
m, l – стороны дельтоида,
r – радиус в случае вписанной окружности.

Как найти площадь четырехугольника — параллелограмма
Если выпуклый многоугольник имеет 2 пары непересекающихся сторон, то перед вами – параллелограмм.
Общее выражение
Для определения площади данного вида фигуры потребуются:
- Сторона четырехугольника и высота, на нее опущенная: S = k*h(k),
k – сторона фигуры,
h(k) – высота к ней. - Длина двух сторон, имеющих одну вершину, и градусная мера угла при данной вершине:
S = l*k*sinϕ,
k, l – стороны многоугольника,
ϕ – угол между ними. - Диагонали фигуры и угол, полученный как результат их пересечения: S = d1*d2*sinβ/2,
d1, d2 – диагонали,
β – угол — результат их пересечения.

Ромб
Данный четырехугольник – частный случай параллелограмма, имеющий 4 равные стороны. Поэтому выражения, справедливые для параллелограмма, верны и для него. Тогда
- S = k*h(k),
k – сторона фигуры, h(k) – высота к ней. - S = k 2 *sinϕ,
k – сторона четырехугольника, ϕ – угол между сторонами. - S = d1*d2/2 (т.к. диагонали фигуры при пересечении образую прямой угол, а sin90° = 1),
d1, d2 – диагонали многоугольника.

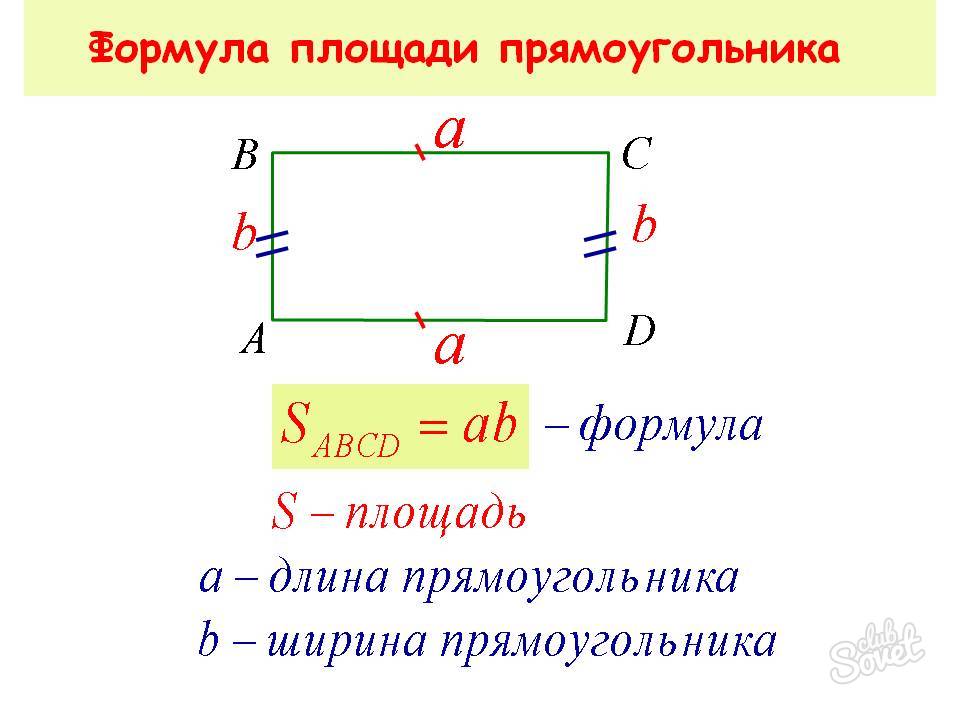
Прямоугольник
Такой многоугольник имеет 2 пары равных сторон, а градусная мера его углов – 90°. Для нахождения его площади справедливы следующие выражения:
- S = k*l,
k, l – стороны фигуры. - S = d 2 *sinβ/2,
d – диагонали четырехугольника, β – угол – результат их пересечения. - S = 2R 2 *sinβ,
R – радиус в случае описанной окружности.
Квадрат
В данном случае у соотношения, полученные на предыдущем этапе, приобретут следующий вид (т.к. стороны такого вида прямоугольника равны):
- S = k 2 , k – сторона фигуры.
- S = d 2 /2, d – диагональ квадрата.
- S = 2R 2 , R – радиус в случае описанной окружности.
- S = 4r 4 , r – радиус в случае вписанной окружности.
